Mathematical models of process behavior can be used to improve the design and performance of feedback controllers.
 In its simplest form, a mathematical model is an equation that relates the value of one variable to another. Properly constructed, a model can describe the behavior of a process in quantifiable terms. For example, Einstein’s famous equation E=mc2 models the process of converting matter into energy. It uses the speed of light (c) to describe how much energy (E) will be produced by annihilating an object of a given mass (m).
In its simplest form, a mathematical model is an equation that relates the value of one variable to another. Properly constructed, a model can describe the behavior of a process in quantifiable terms. For example, Einstein’s famous equation E=mc2 models the process of converting matter into energy. It uses the speed of light (c) to describe how much energy (E) will be produced by annihilating an object of a given mass (m).
More complex models for more complex processes involve more variables and more elaborate mathematical relationships, but all models can be decomposed into four basic components: input variables, output variables, constants, and operators. The output variables are the unknown quantities that the model is designed to deduce from the values of the known inputs. In Einstein’s equation, "E" is the output, and "m" is the input because the mass of the object can be measured to predict the energy that will result from its annihilation.
The value of "c" in Einstein’s equation is a constant. Its value always equals the speed of light in a vacuum no matter what object is being annihilated. Constants generally represent the fundamental laws of physics, chemistry, economics, or other first principles that govern the behavior of the process. Mechanical process models may include a coefficient of friction that is characteristic of the materials involved; electrical process models may include the resistance, capacitance, and inductance of a circuit; and astronomical process models often revolve around the universal gravitational constant.
Operators define the mathematical manipulations required to compute the value of the outputs from the inputs and the constants. They can be as simple as the multiplication and squaring functions that appear in Einstein’s equation or as complex as Laplace transforms and statistical distributions.
An industrial example
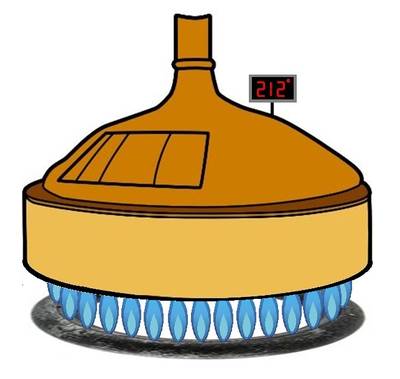
Consider the brew kettle shown in Figure 1. According to Fourier’s Law, heat will flow from the burners into the kettle at a rate proportional to the difference in their temperatures. Mathematically, this phenomenon can be expressed with a process model or input/output (I/O) relationship as shown in Equation 1:
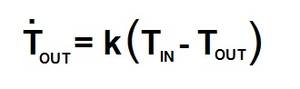
The input TIN and the output TOUT are the temperatures of the burners and the kettle at any given time and ṪOUT is the derivative or rate of change of the kettle temperature at the same instant.
The constant of proportionality "k" represents the rate at which the kettle temperature will increase when the burner temperature exceeds the kettle temperature by 1 deg. Its value is determined by a variety of factors, including the kettle’s shape and construction, the thermodynamic properties of the kettle’s contents, and the ambient temperature. The value of "k" that best represents the behavior of a particular brew kettle can be deduced from an analysis of the applicable first principles, or it can be measured empirically by watching the process perform.
Using the model
Creating an accurate model for a process is only half the battle. The real challenge for the control engineer is designing a controller that makes best use of the model’s ability to predict the output that will result when a control effort is applied to the process’s input.
The brute force method is trial-and-error. The controller guesses what the next control action should be and applies it to the model to see if it will produce the desired output. If not, it keeps trying until it finds that it has guessed correctly. Because this search can be accomplished in computer time, the controller can try thousands of possible control efforts before the time comes to apply its final choice to the actual process.
On the other hand, a strictly trial-and-error method is horribly inefficient. A more intelligent approach would be to choose each guess according to the results of the previous trial, thus honing in on the correct choice iteratively.
An even simpler approach would be to use a model, such as Equation 1, that can be solved and inverted mathematically. It then becomes a straightforward matter to feed the desired output value into the inverted model and directly calculate the control effort required to achieve it. Unfortunately, this obvious technique can produce numerically unstable results for reasons that are not at all obvious.
Implicit techniques
The foregoing are all explicit methods for incorporating a process model into the controller’s operations. Implicit techniques that use the model only for the design of the controller are much more common.
For example, proportional, integral, and derivative (PID) tuning rules translate the model’s constants into suitable values for the controller’s PID parameters (see "Loop Tuning Fundamentals," Control Engineering, July 2003). A touchy process that the model shows to be highly sensitive to the controller’s efforts would be assigned conservative tuning parameters by most tuning rules. Conversely, a sluggish process would merit more aggressive tuning parameters. The controller never uses the model to compute anything directly, but the model’s ability to predict how the process will respond to a control effort ends up being implicitly incorporated into the controller’s tuning.
The more sophisticated controller design techniques that are traditionally taught in academia—lead/lag, pole placement, setpoint tracking, etc.—also use the process model implicitly to identify the behavior of the process. However, instead of plugging the model’s constants into a fixed set of tuning rules, these techniques use the dynamic characteristics of the model to produce a controller that meets some closed-loop performance criteria.
Other applications
Process models are useful for more than controller design problems. They can be used to create virtual sensors that measure one set of variables and deduce the values of another set mathematically. They can also be used to simulate the behavior of the process when testing a proposed controller before commissioning it.
Perhaps the most profitable application for process models (in the chemical and petrochemical industries, at least) is constraint management. Constraints are the physical limitations that determine the maximum allowable values for the process variables, such as the capacity of a tank, the temperature limit of a reactor, a pipe’s maximum flow rate, etc.
A chemical process generally operates most profitably when running as hard as it can within its physical limits. The controller’s job is to maintain the process variables in the high-profit range without allowing them to violate their respective constraints. An accurate model of the process allows the controller to determine in advance where the process variables are headed and take preemptive action to prevent impending constraint violations. Without the foresight offered by the process model, the controller would have to maintain the process variables well away from their constraints (and in a less profitable range) just to maintain a safety margin.
Process optimization works much the same way. When different elements of a process compete for resources, such as electricity, steam, or raw materials, a model of the overall process can demonstrate the economic effects of rationing the resources in different combinations. The controller can determine in advance which rationing strategy is most profitable and go about implementing it without having to waste time and resources guessing.
 Modeling the process
Modeling the process
A wide variety of techniques are available for determining the mathematical model that best describes a process’s input/output (I/O) relationship, an exercise known as modeling or identifying the process. Perhaps the most common technique is a step test that involves raising the input abruptly, holding it steady, and recording the output values that ensue.
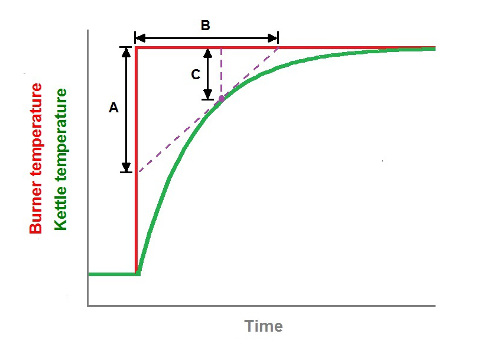
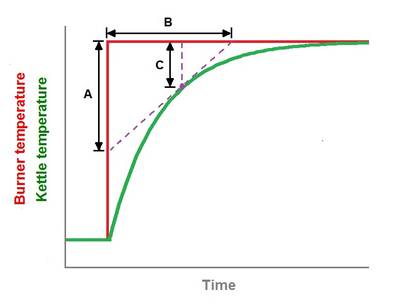
Plotting those output measurements versus time yields a trend of the process’s step response that can be analyzed to determine the appropriate form for the process model. The shape of the first order lag step response is characteristic of all process models, such as Equation 1 with a derivative operator (see Figure 2).
The coefficient "k" can be read from the graph by drawing a line tangent to the step response at any convenient point. If the slope of that tangent line is A/B and the difference between the burner and kettle temperatures at that instant is C, then k must be the result of Equation 2:
k = A/BC
If the process is in fact governed by Equation 1, the value of "k" computed by Equation 2 will be the same no matter what point is chosen for the tangent line. But if significantly different values of "k" result at different points along the graph, Equation 1 is probably not a good choice for the process model. This is one validation method that can be used to check if a proposed process model accurately represents the process behavior.
Vance VanDoren, PhD, PE, is a Control Engineering contributing content specialist. Reach him at [email protected]. Edited by Jack Smith, content manager, CFE Media, Control Engineering, [email protected].
Key concepts
- A model can describe the behavior of a process in quantifiable terms.
- Process models are useful for more than controller design problems.
- Models are directly related to PID tuning rules.
Consider this
When evaluating the use of process modeling for more than controller design problems, you should understand how they can be used to simulate the behavior of processes when testing a proposed controller.
ONLINE extra
See related articles below about process modeling.


