An absolute encoder, while necessary and useful, can offer some challenges if the user doesn’t understand the mathematics of how they work and function.
There are numerous applications that employ encoders in automation control. The purposes are too numerous to list. However, there is one type of encoder that is used that does offer some challenges to those unfamiliar with the mathematics of how they work: The absolute encoder.
An absolute encoder provides a unique number that reflects the angle of rotation, typically coupled to a shaft. These encoders will typically be characterized by their resolution, reflected in the number of increments per revolution, and the type of output, either binary or Gray code. The resolution is important in that this reflects the number of slices that the full rotation of the shaft is cut up into; examples are 16 (4-bit), 256 (8-bit), 4096 (12-bit), etc. The type of encoding is relevant to how the sensor is configured which we will not be getting into this aspect at this time. Suffice it to say that the end result is simply a number in the controller that is monitoring the encoder.
For the purpose of this example, we will be assuming an 8-bit resolution. This is designed to primarily keep the numbers and bit patterns manageable.
Provided that the encoder never makes a full revolution, there is no need to go much further. However, this is almost never the case. As such, we have to be concerned with how to determine either the amount of rotation that has been experienced or what is the final encoder value based on desired rotation. The fact that the encoder will "rollover" can give those unfamiliar with binary math some concern, which has led to complex code being written to address this issue. The good news is that this does not need to occur; this is where binary arithmetic can step in and save the day.
For the encoder in question, the range of values returned will range from 0 to 255 (8-bit). The controller type that this unit is connected to is assumed to support various bit resolutions with its decimal numbers and 2’s complement numerical handling. We will also assume a "forward" rotation; the opposite will be mentioned later. Now that the stage has been set, let’s take a look at the numbers.
For the first example, let’s assume an initial value/reading of 192 and the new value of 225. This is very simple (assuming that it didn’t make a complete revolution) and is easily handled with subtraction. 225 – 192 = 33.
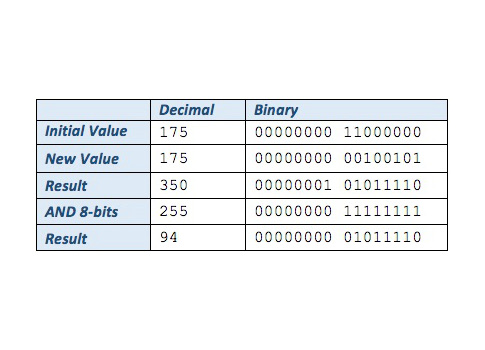
The next case is a bit more complicated. In this case the encoder has rolled over.
Depending on the type of controller there might be more than 16 bits in the binary representation; the operations will be the same, however.
In these cases, there will be logic applied that tries to determine if there was a roll over and subsequently compensating with some further math. While the additional math cannot be avoided, the additional logic can. The use of a logical AND instruction produces the desired result. Since this is an 8-bit encoder, we simply need to perform a Boolean AND operation with the decimal number 255 (binary 11111111).
In this case, the encoder advanced by 101 units.
The elegance of this is that the principle works in the other direction as well. In this case we want to see what the new reading would be if we want to advance by a specific number (this is an addition operation).
By applying this property continuously to the equation, whether through addition or subtraction, allows for consistent code to be developed with no additional branching logic to be applied to keep the code as concise as possible. This step can be applied iteratively in the case of multiplication.
It should be evident at this point that whether the encoder is coupled with the shaft in either rotational direction, the only thing that needs to be considered is whether or not addition or subtraction is to be applied given the operation (determining the amount of rotation or calculating the new position). This method works for any binary consistent encoder, meaning the values are evenly divisible on a bit boundary. Values such as 0 to 355 (for degrees) will not work in the same way.
Not only does an absolute encoder ensure complete angular reproducibility, but the operations required are simple and straightforward. We just need to keep this simple mathematical principle in mind.
This post was written by Jeff Monforton. Jeff is a senior engineer and consultant at Maverick Technologies, a leading automation solutions provider offering industrial automation, strategic manufacturing, and enterprise integration services for the process industries. Maverick delivers expertise and consulting in a wide variety of areas including industrial automation controls, distributed control systems, manufacturing execution systems, operational strategy, business process optimization, and more.
Maverick Technologies is a CSIA member as of 7/12/2016.



