Inside Machines: Learn how to control machine resonance—the “white noise” generated by machine motion—in servo-driven printing and converting machines. Intelligent servo drives provide advanced programming tools, diagnostic features, and integrated filtering capabilities to combat mechanical resonance.
Printing and converting machines driven by distributed servo drives and motors provide several key benefits over gear-driven motors. Each axis is directly driven by its own servo motor, eliminating the need for line shafts, gear sets, and oil baths (and associated maintenance).
Product changeover is much faster and easier, as the motors can change speeds and cam profiles with the press of a button, instead of physically replacing gear sets or mechanical cams. In addition, process controls for registration and tension can be handled by directly changing position or velocity command values of the servos, without needing compensators or other auxiliary hardware to affect the motion.
But unlike a gear set, a servo motor usually requires tuning to achieve optimal performance and overcome mechanical resonance. In the position control loop, the commanded position is compared to the actual position. The difference is multiplied by a factor (gain) and the output becomes the command for the velocity control loop. The output of the velocity loop, in turn, becomes the command for the current loop, and the output of this final loop dictates the direction and magnitude of the current that is delivered by the servo drive to the motor windings.
All three control loops have several types of “gains” associated with them, and tuning is the process of adjusting these gains until the actual motion is matched as closely as possible to the desired motion. In practical terms, this results in colors that are tightly registered with each other for a clear printed image, or a die-cut that is matched precisely with the speed of the paper feed so that no tearing or buckling of the paper occurs. Higher gain generally results in higher bandwidth (responsiveness), but too much gain will result in overshoot and instability.
Mechanical resonance
In theory, the ideal control loop gains based on the load characteristics (such as inertia, stiffness) and desired response may be calculated. But some factors can limit these gain values and prevent the application from achieving the desired bandwidth. For example, if the sampling frequency of the control loop is too low, the output will never settle on a stable value. But a more challenging issue is mechanical resonance.
Mechanical resonance results from the excitation of the natural frequency of a mechanical system. The natural frequency is one where vibration or “ringing” occurs with minimal stimulus, and is an inherent characteristic of a mechanical system. The couplings, bearings, gears, and machine frame can all influence this frequency. Resonance can reduce the life and product quality of a mechanically driven (line shafted) machine, and its effects are particularly noticeable at certain machine speeds that are related to the natural frequency. On distributed servo-driven machines, these effects can be further exaggerated when the control loops act upon feedback that contains significant components of the natural frequency. Since there is already a natural amplification that occurs at this frequency, compounding it with the gain of the control loop can easily cause resonance to manifest in the form of excessive vibration and instability. At best the product quality will suffer and the components of the machine will wear and fail sooner. At worst the machine will not run without motors overheating or frequent web-breaks.
Natural frequencies
When problems arise due to resonance, one might use accelerometers to collect vibration data. Supporting software can be used to analyze the data and distill the natural frequency of the machine or various substructures. Then modifications could be made, such as adding support beams to stiffen the machine structure, or using higher grade couplings or bearings, in an effort to move the natural frequency out of the range of machine operation. These mechanically oriented means of diagnosis and correction require tools and expertise, and incur additional project costs. Alternatively, a “try it and see” approach of making changes and hoping for good results can be time consuming and fruitless.
Approaching this from the control side, the gain of the velocity loop in the servo drive can be lowered. Focusing on the velocity loop shows the obvious effects of resonance in the velocity feedback, amplified by the velocity loop. In some cases, resonance may be mild enough that simply lowering the velocity loop gain will avoid instability while providing enough ability to control the motor adequately and meet the demands of the application.
In other cases, the gain would have to be so low to avoid the problem that the servo performance becomes noticeably compromised. This may mean that a print cylinder has high position deviation—causing the print registration to move in and out of tolerance from image to image (some images look good, others are blurry). Or a tension roll may have inadequate velocity regulation, resulting in fluctuations that cause reduced print quality, stretched or shrunken images, and unevenly wound rolls.
With intelligent servo drives, the effects of resonance can be overcome without compromising performance or investing additional resources. A converter drive can be used to control a synchronous ac motor. An inertia wheel is coupled to the motor shaft to provide a load for testing. The wheel is slightly unbalanced and attached to the motor using only a screw that passes through the center hole of the wheel and into the threaded bore of the motor shaft. There is no coupling device to dampen vibration or compensate for misalignment.
When the motor is first enabled, there is an audible, oscillatory “humming” that indicates some instability in this simple mechanical system. Raising the velocity loop proportional gain above the default value causes the humming to grow louder. Not only is this unpleasant, but it tells us that the motor is on the verge of going completely unstable—causing the drive to fault with a position or velocity loop error. Lowering the gain will dampen the oscillation, but at the cost of lowering the performance. This cost would be unacceptable for the plate roll of some flexographic printing machines, for example, that tolerate no more than 0.002-in. of registration error for the more demanding print jobs. Figure 1 shows the position deviation seen while running at 500 rpm using default gains. Error of as much as .065 degrees peak-to-peak is observed. On a 24-in. circumference cylinder, this would correspond to 0.0043-in. of error at the surface. Increasing the gains can improve upon results after overcoming the oscillation.
White noise test
To see the frequency response, use the drive-integrated oscilloscope software utility. This collects and displays drive data at a resolution of 250 micro-seconds. The captured data is stored in the drive over a fixed duration, and then uploaded to the software. The data is deterministic and is not dependent on communication speeds or scan times. There are hundreds of drive parameters to choose from, but for this test, motor feedback velocity is most applicable. While the motor is vibrating, software can be used to capture one second’s worth of data and upload results in the oscilloscope window, displayed as a function of time. To address the frequency domain, select an FFT (Fast Fourier Transform) plot to display the signal amplitude as a function of frequency (Figure 3). Ideally, there would be a relatively flat curve across the frequency range. In this case, there’s a noticeable spike around 1075 Hz. This is the primary source of the disturbance.The first step is to identify the resonant frequency by doing a “white noise” test. Using Rexroth’s Drive-Integrated Command Value Generator (Figure 2), a noise signal can be applied to the torque command input of the motor. Using a predefined amplitude, the generator outputs positive and negative torque values alternating at random frequencies. This causes the motor to vibrate, producing a white noise similar to TV or radio static. Without the use of a hammer or mallet, the motor is “hitting” the mechanics with a wide range of frequencies to see if one or more generates a stronger response than the others.
Filtering, control loop
After identifying the resonant frequency, a velocity loop filter may be used to minimize the impact on the control loop. In addition to a smoothing time constant (low-pass filter), the drive can provide additional filtering options. Up to four filters can be applied simultaneously. For this test, the frequency is high enough that a simple low-pass filter may be effective. But often the problem frequencies are in the 200-300 Hz range. A low-pass filter that effectively dampens frequencies in this range will also have velocity loop responsiveness. This is especially true for a direct drive motor, where the bandwidth of the velocity loop could approach the range of the disturbance. Rather than using a “broad brush” approach, a more targeted solution would focus on the problematic frequency while minimizing the impact elsewhere in the frequency spectrum. The best solution is a band rejection filter, sometimes called a notch filter.
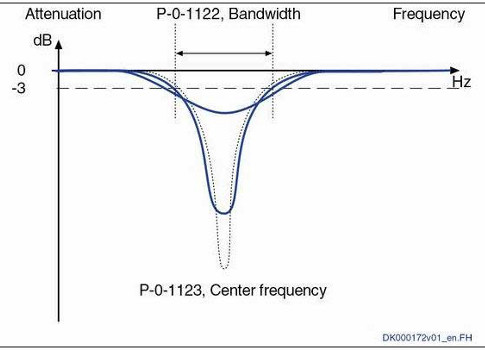
The band rejection filter is parameterized using a center frequency and bandwidth. Signals around the center frequency are heavily attenuated, but the attenuation drops off dramatically when approaching either end of the bandwidth (Figure 4).
Based on the results from the white noise test, apply the filter with a center frequency of 1075 Hz and a bandwidth of 100 Hz. The smaller the bandwidth, the greater is the suppression of the resonant frequency. But a narrow bandwidth in turn requires greater accuracy in setting the center frequency. In practice, the default value of 100 Hz usually works well. As soon as the filter is activated (Figure 5), the audible humming is greatly reduced.
Using the oscilloscope shows graphical evidence of improvement. The plot (Figure 6) shows velocity feedback before (red) and after (blue) the notch filter is applied. Notice how the “noise” in the signal has been reduced by more than half.
4 steps to use intelligent servo drives to filter mechanical resonance
- Understand the fundamental nature of mechanical resonance and natural frequencies—how they arise and interact with control loops
- Use white noise tests to identify the resonant frequency as the starting condition that needs to be controlled through servo drive tuning
- Use filtering to minimize the impact on the control loop
- Tune the position control loop, the velocity loop, and the current loop by adjusting the various “gains” of each loop so the actual motion matches, as closely as possible, the desired motion.
Also read: Technologies for filtering mechanical resonance with intelligent servo drives linked at the bottom of this article.
– Brian Schmidt is senior applications engineer, food, packaging and printing industry sector, Bosch Rexroth Corp. Edited by Mark T. Hoske, content manager CFE Media, Control Engineering and Plant Engineering [email protected].
ONLINE
https://www.boschrexroth-us.com



