Tuning a PID controller correctly can bring the setpoint closer to the constraint with reduced variability.
Process industry plants must optimize regulatory and advanced control to maximize profitability while maintaining safe operation. Regulatory control stabilization is key to achieving these goals. Stabilization can often be improved through closer evaluation of a plant’s regulatory control loops.
Most of these loops are operated by a proportional-integral-derivative (PID) controller. By better understanding how to tune these loops, plant personnel can improve quality and efficiency while ensuring plant safety. Moreover, achieving regulatory control stabilization forms the foundation for advanced process control implementation, which can further optimize operations.
In addition to maintaining safe operation, a stable regulatory control system can increase profitability by reducing emissions and energy consumption, and increasing the life span of equipment. By automating troublesome control loops, the need for manual operations is reduced, saving labor hours and increasing product consistency.
This article offers an introduction on how to achieve a stable, well-tuned regulatory control system, with emphasis on improved PID control.
Control loop basics
In a typical control loop, a parameter, such as temperature or pressure, must be controlled. This parameter is called the process variable (PV). A sensor usually measures the PV, and this measured variable is provided as feedback to the controller in a closed-loop system.
The desired value for the PV, such as 40 F in the case of a temperature control system, is called the setpoint variable (SV). If the PV is only 30 F, for example, the controller will react to adjust its output to increase the temperature.
A constraint is the limit at which the process can be performed safely and efficiency. For example, the heat at 42 F will destroy the compounds in a liquid during a certain process. Therefore, the process must remain below this constraint. However, a process operating at 36 F is so far below the constraint that quality is lost and/or the process becomes inefficient. Thus, the goal is to control the PV and keep it as close to the SV as possible with minimal variability. When variability is minimized, the SV can be moved closer to the constraint, improving operations.
PID controllers
The PID controller is the most commonly used controller type in process plants, with more than 95% of the control loops in a typical plant under PID control. The familiar PID controller can be a great tool for improving quality, energy efficiency, and production.
PID controllers offer good performance in a variety of operating conditions and they can be operated in a simple, direct manner. They can be stand-alone or embedded, and they can be used for one or for many control loops. They can also be combined with sequential logic and advanced control functions to form complex automation systems.
The PID algorithm consists of three basic elements: proportional, integral, and derivative. The setting for each of these three elements is varied to achieve an optimal response: to maintain the PV as close to the SV as possible with minimal variability. Each element is linked to a certain task that has a specific effect on the control loop.
A PID controller receives the measured PV data from a sensor, and then determines the difference (error) between the measured PV and the desired SV. It then computes the desired controller output or manipulated variable (MV) based on the error. The MV in turn acts on the final control element (for example, a steam valve), which in turn affects the process to change the PV (see Figure 1).
There are many techniques for calculating the tuning constants for PID controllers. Most are based on developing a mathematical model for the combined final control element, process, and measurement.
The model for describing the controller is simply the PID Algorithm. If a model can be determined for the process (final control element, process, and measurement), then a mathematical model for the entire loop is in place. At that point, tuning the controller becomes a matter of matching the controller tuning constants (P, I, and D) to the parameters of the process model, and optimizing the three PID constants to produce a desired response.
In the real world, the controller output is usually not the only signal that affects the system. There may be elements within the environment that cause deviations, such as ambient noise. These elements are called disturbances. While disturbances must be factored in when controlling the process, they are also intentionally introduced on a temporary basis as an initial step to tune the controller.
Tuning a PID controller
The process of tuning a PID controller involves five steps:
- Introducing a disturbance into the control loop
- Fitting the resulting response to a mathematical model
- Using tuning correlations to calculate controller parameters
- Implementing the new P, I, and D parameters
- Documenting the results.
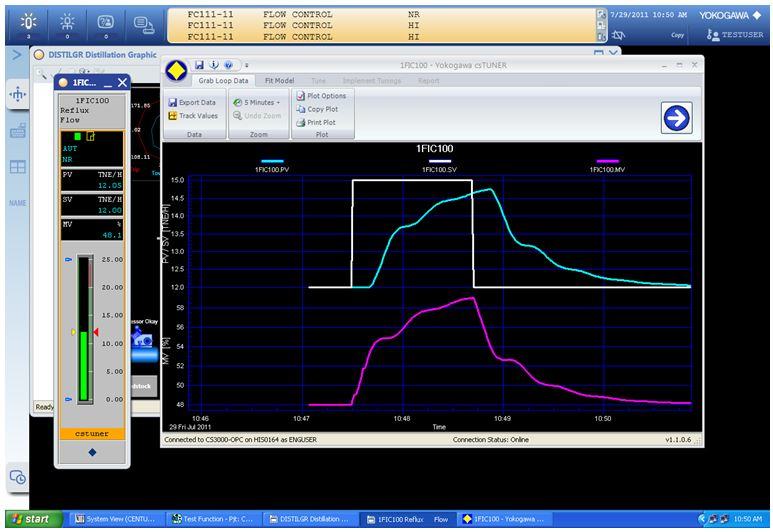
The first step in tuning the PID controller involves inserting a disturbance that creates a new controller output (CO) into the loop. This is called a bump test. The disturbance introduced into the loop must be large enough to force a clear PV response, and the response must be large enough to distinguish it from any noise in the system. Unmeasured disturbances can corrupt the PV data, so larger CO bumps are better (see Figure 2).
Self-regulating process vs. integrating process
Any number of model types is possible for describing a process. But before choosing a model, one must first determine if the process is self-regulating or integrating (non-self-regulating). This determination is essential in tuning a controller because the different processes require different mathematical models.
After a change in the CO is introduced, a self-regulating process will eventually find a steady state as long as the CO and disturbance variable remain steady, as the process has an internal method of regulating the PV that balances the change in the CO. For example, in a flow loop, if a valve is opened an additional 10%, the flow will increase to a new value and will stay at that value until the valve is moved again. Most processes are self-regulating.
However, in an integrating process, the PV will keep changing unless the CO is returned to its original position. With an integrating process, the PV will continue to rise or fall in a linear fashion in relationship to the CO change. This means an integrating process can be difficult to control. An example of an integrating process is changing the liquid level in a tank. If more flow is introduced into the tank, the level will keep rising; if more flow is let out, the level will continue decreasing.
Tuning control loops for self-regulating processes tends to be easier than tuning integrating processes. Negative consequences can happen very easily and quickly if an integrating loop is tuned incorrectly. The inability to achieve equilibrium after a change in the CO is introduced in an integrating process could lead to problems, for example, a liquid overflowing or running dry, which could cause equipment (pump) damage, environmental damage, or significant safety issues.
Self-regulating processes require both proportional and integral (and occasionally derivative) control modes for good performance. Despite their nomenclature, integrating processes rely much less on the integral control mode. Different tuning rules must be applied because the process models are different.
Using modeling
After the bump test is performed and the type of process involved is determined, the next step involves fitting a model to the data. Modeling is one of the best ways to understand process data. A first order plus dead time (FOPDT) dynamic process model is usually sufficient to describe the process response and allow calculation of good tuning constants.
In this model, the PV is the measured process variable and the CO signal is the manipulated variable. The FOPDT model is simple (low order and linear), thus it only approximates the behavior of the real process. It’s represented by the following equation:
Lumped parameter process model
The lumped parameter model is an FOPDT model. This model describes the process response with simple linear equations comprised of three parameters: gain (), time constant (), and dead time ().
For the lumped parameter model, two forms of models are required depending on the nature of the process control loop: the self-regulating process (flow, temperature, etc.) and the integrating process (level).
Because an integrating process is more difficult to control, a different model must be used to describe this type of process, which is described by this equation:
Tuning correlation
There are many different tuning correlation methods used to calculate the PID tuning constants.
Ziegler-Nichols and Cohen-Coon are the two most popular techniques for calculating tuning constants. These two techniques emphasize speed of response. Internal model control (IMC), also referred to as the “Lambda rules,” offers a robust alternative that balances speed of response with controller stability or robustness. IMC tuning can be used for linear and nonlinear processes, and it produces a smoother FOPDT response than other techniques.
IMC tuning is based on the concept that ideal control is possible with an exact model of the process. However, a mismatch between the model and the actual process can occur because of external disturbances that affect the process, which can lead to faulty results. As a result, IMC was designed to have methods for compensating for disturbances and modeling error, including filters and compensators in the higher frequency domain where many errors occur in other models.
Like other tuning procedures, a step test must be performed with IMC to determine the process characteristics. After determining the lumped parameter process model, a desired closed loop time constant () for the control loop must be selected.
If the closed-loop time constant is too large, a slow control loop will result. Therefore, a smaller value will create a faster control loop. But if the closed-loop time constant ( is set to be shorter than the FOPDT process time constant (), the advantages of IMC tuning will disappear.
Generally, the value for should be set between one and three times the value of (). In many cases, = 3 x is optimal to achieve a very stable control loop. Therefore, after determining the FOPDT process model, the IMC technique has one single tunable parameter: the closed-loop time constant. The controller speed is made more aggressive or more conservative by changing the closed-loop time constant.
IMC has one drawback in that the controller’s integral time is set to equal the process time constant. A process with a very long time constant means the controller will also have a very long integral time—and long integral times lead to very slow recoveries from disturbances.
Properly tuning a PID controller isn’t a simple process, but it’s one of the best methods for improving productivity, quality, and safety in a process. By achieving a stable regulatory control system through improved PID tuning, the SV can be safely moved closer to the constraint while reducing the variability of the PV, thus reducing inefficiencies in the process.
However, collecting data and performing all of the modeling mathematics can be difficult and time consuming. Fortunately, advanced software can simplify PID controller tuning and reduce the possibility of error (see Figure 3).
Whether PID loop tuning is performed manually or with assistance from loop tuning software, the resulting improvements in the performance of each control loop will lead to significant overall performance gains throughout the process plant.
Dr. Merle Likins, PE, retired, has undergraduate and graduate degrees in chemical engineering from the University of Louisville. He is a licensed professional engineer in five states and has more than 35 years of experience in process automation. Dr. Likins has an extensive background in petroleum and chemical processes. He also has many years of experience in multivariable control, online process models, and online optimization. Prior to retirement, Dr. Likins worked with Yokogawa Corp. of America from 1992-2013.
This article appears in the Applied Automation supplement for Control Engineering and Plant Engineering.



