Sometimes a process is easier to control if it “leaks.” Here’s a look at why.
What do water tanks and servo motors have in common? For feedback control purposes, they’re both integrating processes, which means they’re both governed by mathematical relationships that produce the behavior shown in the graphic "Input/output relationship for an integrating process."
An integrating process produces an output that is proportional to the running total of some input that the process has been accumulating over time. Alternately, an integrating process can accumulate a related quantity proportional to the input rather than the input itself. Either way, if the input happens to turn negative, an integrating process will start to relinquish whatever it has accumulated, thereby lowering its output.
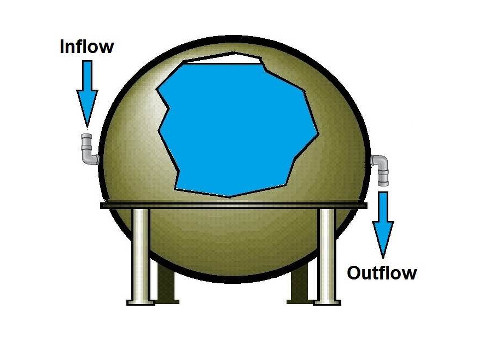
For the water tank shown in the "Integrating process example," input is the water flowing into the tank—the net flow from all incoming streams minus outgoing streams. The output is the level of water the tank has accumulated. As long as net inflow remains positive (more incoming than outgoing), the output level will continue to increase as the tank fills up. If net inflow turns negative (more outgoing than incoming), output level will decrease as the tank drains.
Servo motors have an entirely different accumulation mechanism, but the same effects. A servo motor’s input voltage generates torque, which accelerates a load around the shaft. The resulting rotation turns the load a bit more for every instant input voltage is non-zero. The load’s net position results from the accumulation of all those incremental rotations, each of which is proportional to input voltage at that instant. As long as input voltage remains positive, the output position will continue to increase. If input voltage turns negative, the output position will decrease as the shaft turns backwards.
The water tank and servo motor also behave similarly in that fixing their inputs at zero will fix their outputs at whatever values they’d reached up to that point. The tank’s water level will remain unchanged as long as incoming flow exactly matches outgoing flow (typically when both are zero), and the servo motor’s shaft will remain in its last position as long as input voltage is neither positive nor negative.
This is a defining characteristic of all integrating processes. They can accumulate their inputs and subsequently disperse them without suffering spontaneous losses to the surrounding environment. Accumulation and dispersal rates can vary considerably from process to process, and the two rates can be different within the same process depending on the effects of friction and inertia. But once a chunk of input has been successfully added to the running total, it will stay there until a negative input removes it. That is, a drop of water that has entered the tank will remain within (or be replaced) until outflow exceeds inflow.
Losses as well as gains
Other processes can lose what they’ve accumulated without the benefit of a negative input. A leaky tank will lose water no matter how the inlet and outlet valves are set, and a servo motor rotating against a torsional spring will lose position whether input voltage is positive, negative, or zero.
Such processes can reach an equilibrium point where further accumulations are offset by spontaneous losses. If a tank is leaky enough, a given inflow rate will not be able to raise the output level beyond a certain height. If the spring opposing the servo motor is strong enough, it will eventually prevent the shaft from rotating any further.
These are often called non-integrating processes, though "short-term integrating" might be a more apt description. They accumulate their inputs just as integrating processes do but only until they reach an equilibrium point between input and losses, as shown in the "Non-integrating process example."
It’s also somewhat misleading to describe integrating and non-integrating processes as if they are entirely distinct classes. Very few integrating processes are completely immune to spontaneous losses, and some non-integrating processes have very long time constants. That is, they suffer their losses so slowly that an equilibrium point can never be reached. Every process falls somewhere on the continuum from perfectly integrating to decidedly non-integrating. There really isn’t a clear dividing line between the two extremes.
Selecting a controller
As a practical matter, a control engineer must be able to recognize which end of the continuum a given process is closer to in order to choose a suitable feedback control strategy. It is harder for a controller to find an input that will yield a particular output from an integrating process because of the output’s propensity to continue rising or falling as long as the input is anything but zero. Regulating a non-integrating process is considerably easier since the equilibrium point imposes a natural limit on how high the output can go. The controller simply doesn’t have to work as hard to find the right input.
In fact, non-integrating processes are sometimes described as self-regulating because of their ability to achieve a steady state without a controller’s intervention. Still, that is not an entirely accurate description either. The efforts of a feedback controller will still be required to raise or lower the process’s input if the current equilibrium point doesn’t happen to match the desired output.
Fortunately, traditional PI or PID controllers usually suffice for both integrating and self-regulating processes, though their configuration and performance will differ. In particular, any tuning rules that the control engineer might use to select the controller’s P, I, and D parameters must take into account the essentially infinite time constant of an integrating process. Most tuning rules come with two sets of formulas for translating the process’s input/output relationship into tuning parameters-one for integrating processes and one for self-regulating processes. See, for example, "Fundamentals of lambda tuning linked below."
For some applications involving an integrating process, even a simple proportional (P-only) controller will work since the process’s accumulation mechanism performs the same mathematical function as the integrator in a PI or PID controller. The process itself can sometimes provide necessary integral action depending on the controller’s objectives. Specifically, if the controller’s only goal is to find the input required to force the output to match a newly selected setpoint, a P-only control strategy should work well enough.
Close enough
But if the process is non-integrating, a P-only controller will tend to give up before the output reaches the setpoint, leaving a permanent discrepancy between the two. The same steady-state error will ensue if the controller tries to compensate for a load disturbance which occurs when some external force begins to compete with the controller for influence over the process. Steady-state error due to a load disturbance will affect both integrating and self-regulating processes alike.
For example, an unexpected surge in the inflow entering either the impervious tank or the leaky one will increase the net inflow and raise the output level above the desired height. A P-only controller will react by opening the outlet valve further so as to lower the net inflow, but its efforts will be insufficient. The controller will invariably settle on an outlet valve position that leaves the water level too high.
On the other hand, that won’t be a problem if the application doesn’t require the level to be maintained precisely. Sometimes a level controller is only required to prevent the tank from overflowing or draining dry.
As an interesting exercise, consider why a P-only controller leaves a steady-state error when compensating for a load on an integrating process but not when responding to a setpoint change, and why the same controller leaves a steady-state error in both cases when the process is self-regulating. You’ll find the answer is both non-intuitive and mathematically complicated. For a brief explanation of this phenomenon, see "Fixing PID, Part 1 linked below."
Vance VanDoren, PhD, PE is a Control Engineering contributing content specialist.
Key concepts:
- Processes have specific characteristics that affect the way in which they should be controlled.
- Understanding how a process responds to control efforts is a critical step of establishing control strategy.
ONLINE
Read more about loop control and tuning strategy below.



