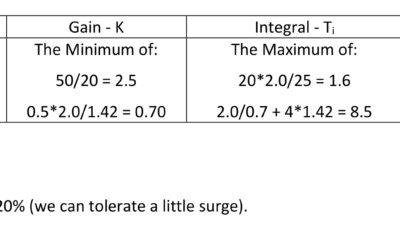
Control loop tuning information, advice and optimization

Learning Objectives
- Review four control methods to optimize PID tuning, according to ChatGPT, are Ziegler-Nichols, Cohen-Coon, Internal Model Control (IMC) and Model Predictive Control (MPC).
- Understand the PID tuning process, according to ChatGPT.
- Discover the importance of having one source of truth for programming and the benefits of open communication for the team.
PID Loop Insights
- PID loops are a type of control system used to regulate and stabilize a process variable.
- They consist of three components: proportional control, integral control and derivative control.
- The parameters of a PID loop can be adjusted through methods such as manual tuning, Ziegler-Nichols method, model-based tuning or auto-tuning to optimize the system’s performance.
What are proportional-integral-derivative (PID) loops, and how should PID loops be tuned? What advice do you have, using engineering and control methods, to optimize proportional-integral-derivative (PID) tuning? Control Engineering asked ChatGPT these questions in February 2023. The following advice was lightly edited for style, and links were added to past Control Engineering coverage on loop-tuning topics. [If you are an engineer with automation and controls experience in PID loop tuning and would like to share your PID expertise, please see https://www.controleng.com/contribute.]
PID loops: What they are and how to tune them
A PID loop is a type of control system algorithm commonly used in industrial, manufacturing and process control applications to regulate and stabilize a process variable, such as temperature, pressure, flow rate or level. PID loops are important in industrial, manufacturing and process control applications because they help maintain a stable and accurate process variable. Three parts of PID loops are:
-
Proportional control (P): The proportional control component responds to the error between the desired setpoint and the actual process variable. It adjusts the control output based on the difference between the desired value and the measured value. The proportional gain parameter determines the strength of this response.
-
Integral control (I): The integral control component corrects for any steady-state error that may persist in the system. It continuously sums the error over time, and the resulting signal is fed back into the control output. The integral gain parameter determines the strength of this response.
-
Derivative control (D): The derivative control component anticipates the future error by measuring the rate of change of the process variable. It can help reduce overshoot and improve the response time of the system. The derivative gain parameter determines the strength of this response.
Proportional, integral and derivative components work together to create a feedback loop that constantly adjusts the control output based on the desired setpoint and the measured process variable. By using feedback to adjust the control output, the system can maintain a stable and accurate process variable, even in the presence of disturbances or changes in the system.
The parameters of a PID loop (proportional gain, integral time and derivative time) can be adjusted to optimize the system’s performance. However, tuning a PID loop can be a complex task that requires knowledge of the system’s dynamics, operating conditions and performance requirements.
PID loop-tuning methods, process
PID controllers are widely used in control systems to regulate and stabilize processes. PID tuning is the process of adjusting the controller’s parameters to improve its performance, and it can be a challenging task for control engineers.
Manual tuning involves adjusting the PID loop parameters (proportional gain, integral time and derivative time) based on trial and error. The operator adjusts the parameters until the system responds satisfactorily. This method can be time-consuming and requires a skilled operator with knowledge of system dynamics.
Ziegler-Nichols method is a popular PID loop tuning method. See more below.
Model-based tuning: This method involves using a mathematical model of the system to tune the PID loop. The model is used to predict the system’s behavior under different PID loop parameters, and the parameters are adjusted based on the model’s predictions. Model-based tuning can be more accurate and efficient than manual tuning, but it requires a strong understanding of the system’s dynamics and a valid model.
Auto-tuning: This method involves using software algorithms to automatically adjust the PID loop parameters. Auto-tuning methods vary in their complexity and accuracy, but they can be useful for quickly finding a good starting point for manual tuning or for tuning a system with unknown dynamics.
The choice of tuning method depends on several factors, including the system’s dynamics, performance requirements and the operator’s skill level. It is essential to carefully consider the trade-offs between response time, stability and overshoot when tuning a PID loop. See about loop-tuning optimization, below.
When tuning a PID controller, it is important to consider the process dynamics, control objectives and performance criteria. A good starting point is to use a tuning method, such as the Ziegler-Nichols or Cohen-Coon method to get initial values for proportional gain (Kp), integral time (Ti) and derivative time (Td). Then, use simulation or real-time testing to evaluate the controller’s performance and adjust the parameters accordingly.
It is also important to understand the limitations of PID control and consider advanced control methods such as IMC or MPC if the process is highly nonlinear, has multiple inputs and outputs or requires precise control.
Four control methods to optimize PID tuning
Ziegler-Nichols, Cohen-Coon, Internal Model Control (IMC) and Model Predictive Control (MPC) are engineering and control methods that can be used to optimize PID tuning.
-
Ziegler-Nichols method: This is a classic tuning method that uses step response data to calculate PID parameters. It involves setting the controller’s Kp, Ti and Td to specific values based on the process dynamics. This method is simple and effective for many systems, but it can lead to overshoot or oscillations in some cases. It involves first setting the integral and derivative gains to zero and increasing the proportional gain until the system oscillates at a constant amplitude. The critical gain at which the system starts to oscillate is noted, and the integral and derivative gains are adjusted according to a set of rules to obtain optimal tuning.
-
Cohen-Coon method: This method is based on the process reaction curve and can be used to determine PID parameters for first-order and second-order systems. It provides a good starting point for PID tuning, but it can lead to instability in some cases.
-
Internal Model Control (IMC) method: This method is based on the concept of an internal model that replicates the process dynamics. It can be used to calculate PID parameters that provide a good balance between stability and performance. This method is suitable for systems with long time constants or integrating processes.
-
Model Predictive Control (MPC) method: This is an advanced control method that uses a model of the process and a cost function to calculate optimal control actions. It can be used to optimize PID parameters in real-time, taking into account process disturbances and constraints. MPC is suitable for complex processes and can provide better performance than traditional PID control.
This content was created with ChatGPT. Due to limits of AI tools, content was edited and reviewed by Tyler Wall, associate editor for CFE Media and Technology, [email protected]; and Mark T. Hoske, content manager, Control Engineering, [email protected].
KEYWORDS: PID tuning optimization, ChatGPT
CONSIDER THIS
How many of your control loops are in manual, not optimized by available software?