Understanding the matrix for APC improvements

The dominant aspect of process control activity for the next couple of decades will (most likely) be multivariable control. This is the next logical step in process automation progress. Better tools are making advanced process control (APC) methods available to more applications.

After several decades of multivariable control activity, the conventional multivariable control paradigm – model-based control (MPC) and real-time optimization – has never evolved into the multivariable control core-competency the process industry needs. It is evident much work remains to be done (“APC’s missing metric”) and more agile tools are needed to do it (“Multivariable control as core-competency.”)

A modern multivariable control paradigm will combine enduring single-loop process control principles that pre-date the MPC era with key multivariable control lessons that have emerged from the MPC era (Table 1). The surviving core multivariable control principles and lessons will be important to know for control engineers. Chief among them is the concept of the matrix for its role in multivariable control, and also for its role in the bigger picture of effective process operation, constraint management, and process optimization.

Advanced process control connections, directions

The first things to know about any controller, whether single-loop or multivariable, are its connections and directions.

In single-loop control, “connections” refers to which transmitter (or other process measurement) and which valve (or other final control element) are connected to the controller. These are often shown on piping and instrument drawings (P&IDs), control system graphics, and in many other types of process documentation. Each context may include additional controller details, but a controller’s connections are always the minimum information necessary to grasp the role of the controller at a glance, that is, which variable is being controlled by which valve (or by which “handle”).

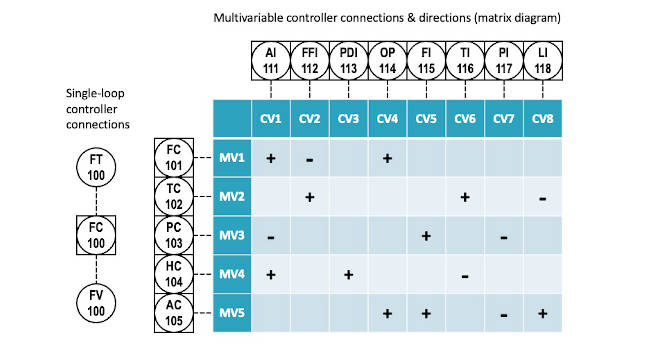
A matrix diagram provides the same information for a multivariable controller (Figure 1). It shows which manipulated variables (MVs) are connected to which controlled variables (CVs), which MVs can be used for constraint control and which CVs can be optimized. As in single-loop control, this is the starting point in understanding the role in process operation of any multivariable controller.

Understanding the control action in APC

The next most essential piece of information is control direction, which is the sign of the process gain. For example, if a single-loop controller output or a multivariable controller MV is increased, does the controlled variable increase or decrease in response?

In single-loop control, this is also known as control action (reverse or direct, respectively). In multivariable control, it is also known as gain direction (positive or negative, respectively). Knowing control direction is necessary to understand the possibilities, limitations and competing interests of utilizing each MV/CV connection for control and optimization purposes.

Control direction is the most enduring aspect of a process model. A single-loop controller may be retuned many times in its life, but its control direction never changes – it is a fundamental consequence of the process design and the controller’s connections. MPC experience also has shown that other model aspects, such as dynamic timing and gain magnitude, may change frequently, but gain direction never does.

Connections and directions together define the basic mechanics and capabilities of a controller. The rest is tuning. Control engineers will often be interested in additional controller details, but connections and directions, in the convenient form of a matrix diagram, comprise the basic information necessary for all members of the operating team to collaborate effectively in multivariable constraint management and process optimization.

Matrix diagrams extend beyond APC applications

In the MPC era, matrix diagrams have often been hidden from view and of interest primarily to APC engineers. Experience has revealed matrix diagrams are an effective tool to concisely diagram the multivariable nature of any process operation. This makes matrix diagrams of primary interest to the entire operating team, including process engineers, operations personnel, distributed control system (DCS) and APC engineers, and all other process operation and optimization stakeholders.

Matrix diagrams have proven to be one of the most effective and appropriate tools to bring all these stakeholders onto the same page when it comes to managing process constraints and achieving process optimization.

In the modern multivariable control paradigm, the genesis of matrix diagrams changes. Instead of originating within APC projects, they originate with process engineers, also known as production or operation engineers, who often have the lead role in steering day-to-day operation towards greater reliability and optimization.

Process engineers also can use matrix diagrams as a communication and discussion tool with the rest of the operating team. Beginning as working sketches developed by process engineers, matrix diagrams can logically migrate into process manuals, training materials, operating procedures, control system graphics, and ultimately into automated multivariable controllers (Figure 2). Not incidentally, as the matrix diagram evolves, it becomes refined and proven in use, so it becomes sanctioned among the operating team before it becomes deployed as an online controller.

Multivariable constraint control and optimization has always been an inherent aspect of nearly all process operations, whether it is carried out manually by the operating team or with the aid of automated multivariable controllers. But prior to the MPC era, industry lacked an effective tool and best practice to capture and share this crucial operating information in a practical and concise format. Bringing the matrix into the mainstream lexicon of process automation may ultimately prove to be the single most important contribution of the MPC era (not models or optimizers: See “Changes in store for APC”).

Theoretical vs. operational matrix design, all process interactions

In conventional MPC practice, matrix design has usually included essentially all MV/CV process interactions as identified through a comprehensive plant step test. Every process interaction, however small or potentially problematic in use, becomes a connection in the matrix. But from an experienced process operation standpoint, a more limited number of MVs are usually known to be effective and proven in operation for the various constraint control and optimization purposes, while many others are known to be problematic and are avoided in operation based on experience and various process and equipment operational considerations.

This is the difference between theoretical and operational matrix design (see “Operational matrix design”). Discussion with process and operation personnel will usually readily reveal which are which – especially if everyone understands the basics of matrix diagrams!

Operational matrix design generally results in multiple, smaller, less dense matrix designs, rather than one large matrix as has been common practice under the theoretical approach of MPC. For example, process engineers and console operators can often explain directly, based on experiences and knowledge, without a plant test, which MVs to use for which constraints and optimization objectives. Process engineers and console operators will rarely mention (or sanction the use of) more than two or three handles for any one purpose; usually it is one or two. As the matrix becomes less dense from this paring of ineffective or problematic handles, it becomes more easily divided into smaller and more manageable parts. This is reflected in Figure 2, which (at a matrix size of 5×8) is smaller and less dense than typical MPC matrix designs (which often have dozens of variables and hundreds of models).

Operational matrix design tips

A good rule of thumb in operational matrix design is if there are more than three models (or connections) in any one matrix column, further review is warranted. There is no hard reason for this, but experience has shown the realities of industrial process and equipment operation tend to have the ultimate effect that more than two or three useful handles for any one objective is rare (except in cases of multiple “parallel handles,” such as heater pass balancing). The bad actor loop metric also can be utilized to help identify existing manual multivariable control practices that have become established within ongoing operation.

APC example: Multivariable control in unexpected places

Example: With the emergence of multivariable control as a core-competency and more efficient and reliable control algorithms, multivariable control can migrate from the supervisory control layer into the base layer. This brings important performance and reliability improvements, especially controller redundancy and high execution speed.

Redundancy means that the question “What if APC is off or unavailable?” no longer needs to be a complicating factor. Instead, small, fast APC applications can be designed to run continuously in the base layer, just like other base layer single-loop or advanced regulatory controls (ARC).

High execution speed means multivariable controllers in the base layer can combine fast controlled variables (CVs) with slow CVs. Conventional APC at the supervisory level often executes at 30 or 60 seconds and only can accommodate correspondingly slow CVs, but many process variables respond much faster than this. APC in the base layer can execute at 1 to 5 seconds, so it can combine fast and slow CVs in one multivariable control matrix design.

Fired heater control, one of industry’s most common multivariable control applications, provides an example (Figure 3).

In the past, fast or critical CVs, such as burner pressure, need to remain in the base layer, while slower CVs, such as excess oxygen or pass balancing, are typically implemented in conventional model-based multivariable controllers at the supervisory level. This split scheme is complex to implement, maintain and operate, and it compromises performance. With APC in the base layer, the entire multivariable control application can be implemented in one combined matrix, bringing significant reliability and performance improvements.

Allan G. Kern, P.E., is owner and consultant at APC Performance LLC. Edited by Mark T. Hoske, content manager, Control Engineering, CFE Media and Technology, mhoske@cfemedia.com.

KEYWORDS: Matrix, advanced process control (APC)

CONSIDER THIS

Should you be using a matrix to optimize more processes?

Do you have experience and expertise with the topics mentioned in this content? You should consider contributing to our CFE Media editorial team and getting the recognition you and your company deserve. Click here to start this process.